자바스크립트에서 소수점을 정확하게 계산할 수 있을까?🤔

자바스크립트에서 부동소수점의 한계와 대안에는 어떤 방법들이 있는지 소개하려고 합니다. 저는 현재 가상자산 커스터디 서비스에서 개발을 진행하고 있으며, 요즈음 암호화폐의 금액 데이터를 이용한 가공 처리 등을 진행하고 있습니다.

이러한 암호화폐는 기본적으로 매우 작은 단위까지 다루어야 합니다. 가장 유명한 비트코인, 이더리움의 단위는 satoshi, wei 이며 각 최대 소수점 8자리, 18자리까지 표현하게 됩니다.

실제 화면에 보이는 데이터를 최대 소수점 자릿수까지 보여주어야 하는 경우는 드물지만, 정확한 금액의 계산 등을 위해 서버로부터 받아오는 값들은 소수점을 자르지(반올림, 내림, 버림) 않고 계산을 해주어야 정확성을 보장해 줄 수 있습니다.

자바스크립트의 한계

소수점 8자리, 18자리 등의 값이 매우 작은 금액의 부동소수점 계산은 자바스크립트에서 문제가 발생합니다. 어떤 문제가 발생하고, 왜 이런 문제가 발생할까요?

알아보기에 앞서 부동소수점이 어떤 건지 먼저 살펴보면 이해가 쉬울 것 같습니다.

부동소수점이란 실수를 컴퓨터에서 표현하고 연산하기 위한 방법 중 하나입니다. 특히 소수와 큰 숫자 또는 매우 작은 숫자를 효율적으로 표현하기 위해 고안된 형식입니다. (더 자세한 내용은 여기)

그중 IEEE 754표준에 따라 정의된 방식이 가장 널리 사용된다고 하며, IEEE 754의 경우 부동소수점을 근삿값으로 표현합니다.

근삿값으로 표현되는 이유는 아래와 같습니다.

컴퓨터는 모든 숫자를 이진수로 표현합니다. 즉 유한한 비트를 사용하므로, 실수를 정확히 표현하기 위해 필요한 모든 소수 자릿수를 저장할 수는 없습니다.
1. 10진수 0.1은 이진수로 정확히 표현할 수 없습니다. 0.1 =0.0001100110011...(무한 반복)
2. IEEE 754에서는 비트를 제한하여 0.1을 근삿값으로 저장합니다.
무한히 많은 실수 값을 제한된 공간에 표현하려면 근삿값이 필요합니다.
유리수와 무리수 표현 등 효율성과 범위를 고려한 현실적인 설계 선택입니다.

이러한 이유로 인해 근사값으로 처리하기 때문에 아래와 같이 근사값을 계산하는 과정에서 오차가 발생하게 됩니다.

1console.log(0.1 + 0.2); // 출력: 0.30000000000000004

부동소수점을 처리하는 방식 중 하나인 IEEE 754 표준에서 근사값으로 처리하는 이유 및 오차에 대해 알아보았습니다. 그렇다면 IEEE 754랑 자바스크립트는 무슨 관계일까요?

→ 위의 오차 예시를 보면 알아차릴 수 있지만, 바로 자바스크립트는 기본적으로 IEEE 754 표준을 사용하여 숫자를 표현하고 연산하게 됩니다.

그러므로 자바스크립트에서 위의 예시와 같이 0.1 + 0.2의 연산도 오차가 발생하게 됩니다. 소수점 자릿수가 크지 않다면 일반적으로 큰 문제가 발생하지 않지만, 이 글의 위에서 소개해 드렸던, 암호화폐와 같은 특별한 경우 즉 소수점 자릿수가 큰 경우에 이러한 자바스크립트의 연산은 오차로 인해 정확성을 보장할 수 없습니다.

해결 방법

이러한 자바스크립트의 부동소수점 계산의 오차를 해결하기 위해서는 크게 2가지의 방법이 존재합니다.

소수를 사용하지 않고, 정수 단위로 변환하여 계산을 진행
오픈소스 라이브러리를 이용하여 처리

먼저 1번 방법인 정수 단위로 변환하여 계산하는 방식은 아래의 코드와 같이 정수로 변환하여 처리합니다.

1const a = 10; // 0.1을 10으로 변환
2const b = 20; // 0.2를 20으로 변환
3const c = 30; // 0.3을 30으로 변환
4console.log(a + b === c); // true

위의 방식은 큰 한계점이 존재합니다. 정밀한 소수의 계산이 아닌 값을 비교하는 경우에만 처리가 가능하다는 점입니다. 단순히 소수의 값을 비교해야 하는 경우에 고려해 보면 좋을 것 같습니다.

다음으로는 라이브러리를 이용해서 처리하는 방식입니다. 이 글에서 소개해 드릴 라이브러리는 decimal.js와 js-big-decimal 라이브러리입니다.

decimal.js

decimal.js는 정밀한 실수 및 소수 계산을 제공하며, 고급 수학 연산(로그, 삼각 함수 등)을 지원합니다.

1// Precision loss from using numeric literals with more than 15 significant digits.
2new Decimal(1.0000000000000001); // '1'
3new Decimal(88259496234518.57); // '88259496234518.56'
4new Decimal(99999999999999999999); // '100000000000000000000'
5
6// Precision loss from using numeric literals outside the range of Number values.
7new Decimal(2e308); // 'Infinity'
8new Decimal(1e-324); // '0'
9
10// Precision loss from the unexpected result of arithmetic with Number values.
11new Decimal(0.7 + 0.1); // '0.7999999999999999'

decimal.js는 정밀도 문제를 해결하기 위해 “임의 정밀도(arbitrary precision)” 방식을 사용하였으며 이는 내부적으로 숫자를 정수와 지수를 분리한 형태로 저장하고 계산하여, 부동소수점 표현의 한계를 해결하였습니다.

기본적으로 모든 계산을 10진수 정밀도로 수행하며, 내부적으로 큰 정수를 다루고, 연산 후 결과를 필요한 자릿수로 조정합니다

→ 10진수 기준으로 수행하기 때문에 2진수 기반의 부동소수점 표현에서 발생하는 정밀도 문제(오차)를 해결할 수 있습니다.

추가로 사용자가 원하는 만큼의 정밀도를 설정할 수 있습니다.

💡 정밀도란?

정밀도는 숫자를 표현하거나 계산할 때 **얼마나 정확하고 세부적인 값을 나타낼 수 있는지**를 의미합니다. 특히 컴퓨터에서 숫자를 표현할 때, 정밀도는 **유효숫자(유효 자릿수)**를 기준으로 하며, 이를 통해 숫자의 정확성을 측정합니다.

js-big-decimal

js-big-decimal은 소수 계산을 단순화하고 가볍게 사용할 수 있도록 제공하는 라이브러리입니다.

1var n1 = new bigDecimal(12.6789);
2var n2 = new bigDecimal("12345.6789");
3var n3 = new bigDecimal("12.456e3"); // 12456

js-big-decimal은 정밀도 문제를 해결하기 위해 “문자열 기반”으로 숫자를 처리하여 부동소수점 표현의 한계를 해결하였으며, 정밀도는 입력값에 따라 동적으로 결정됩니다.

decimal.js vs js-big-decimal ⇒ 두 라이브러리의 차이점

두 라이브러리의 차이점, 그리고 저는 어떤 라이브러리를 왜 선택했는지 공유드립니다. 저는 여러 이유와 사용하는 상황을 고려하며 decimal.js 라이브러리를 선택하였습니다.

첫째, 우선 두 라이브러리는 사용량에 있어 큰 차이를 보이고 있습니다. (24.11.27 기준)

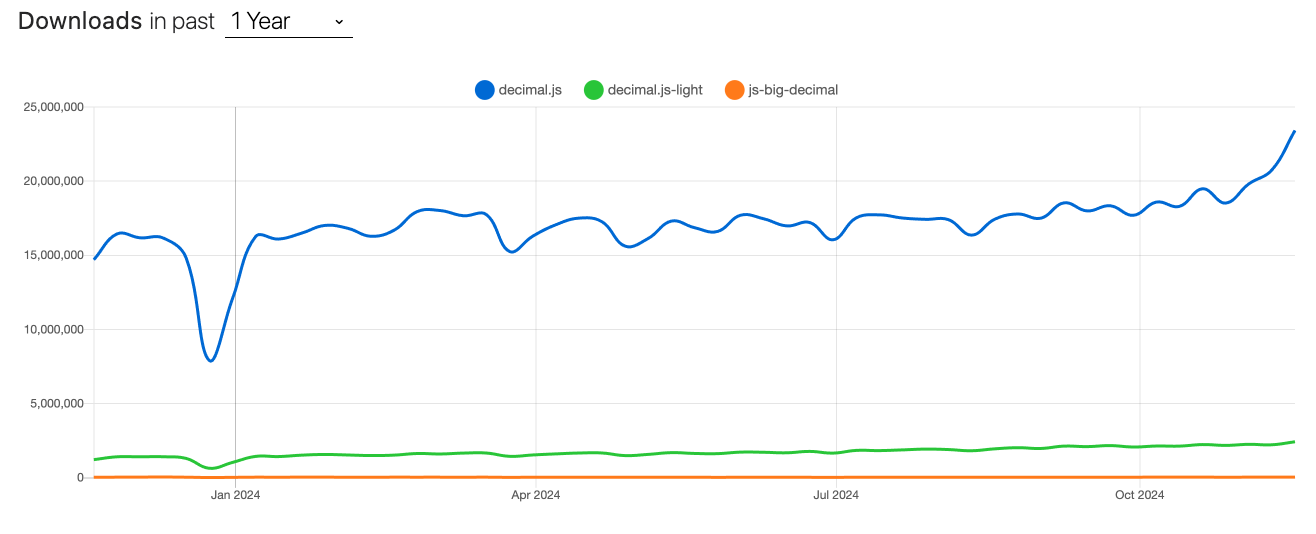
npm trends를 통해 다운로드 수를 비교하면 decimal이 압도적으로 사용량이 높으며 뒤를 이어서 decimal-light(삼각 함수를 사용하지 않는다면 가벼운 decimal.js 버전), js-big-decimal 순입니다.

라이브러리를 선택할 때, 다운로드 수가 높다고 정답은 아니지만, 차이가 많이 나거나, 수치가 크다면 가볍게 무시할 수는 없는 부분 중 하나입니다. 많이 사용한다는 것은 그만큼 잘 동작한다는 증거로 볼 수 있다고 생각하기 때문입니다.

두 번째, decimal.js와 js-big-decimal 라이브러리의 각 특징을 비교했을 때, 자릿수가 많을수록 연산의 속도 차이가 있으며, 기본적인 사칙연산 이외의 계산을 할 수 있는 확장성을 고려하였습니다.

특징	decimal.js	js-big-decimal
내부 저장 방식	10진수 유효숫자와 지수의 조합	숫자를 문자열로 처리
정밀도	기본 20자리, 사용자 지정 가능	문자열 길이에 따라 무제한
연산 방식	10진법 기반 임의 정밀도 연산	문자열 기반 덧셈, 뺄셈, 곱셈, 나눗셈
성능	더 빠름 (정수 기반 계산)	자릿수가 많을수록 상대적으로 느림
고급 수학 연산 지원	지원 (제곱근, 로그, 삼각함수 등)	지원하지 않음

세 번째, 저는 서비스의 특성상 초반부에도 설명했던 암호화폐의 많은 소수점 계산과 암호화폐를 원화, 또는 USD도 변환하거나, 그 반대로 암호화폐로 값을 변환하는 등의 작업을 수행해야 하기 때문에 정밀도, 오류 없는 계산, 연산 성능, 유지 보수 및 확장성을 고려하였습니다.

마무리. 선택에 정답은 없습니다.

이번에 사내에서 소수점 계산을 하는 기능에 대해 작업을 하면서, 자바스크립트의 부동소수점 한계, 그리고 라이브러리까지 살펴봤던 좋은 경험을 공유하고 싶어, 글을 쓰게 되었습니다.

저는 위에 나열한 요소들과 상황을 통해 decimal.js를 선택하였지만, 단순한 소수점 계산 및 자릿수가 적은 상황이라면 js-big-decimal도 좋은 선택지라고 생각합니다. (decimal.js 사이즈는 276kb, js-big-decimal 사이즈는 198kb 입니다.)

이 글을 통해 부동소수점 관련해서 문제를 해결하는 데 도움이 되길 바랍니다. 선택에 정답이 없으며, 각자 상황에 따라 최선의 선택을 통해 문제를 해결하는 것이 중요하다고 생각합니다.

긴 글 읽어주셔서 감사합니다.

참고문헌

사진: Unsplash의Jigar Panchal